Mathematica ile Karmaşık Dinamik Sistemlerin Çözümü, Stabilite Analizi ve Görselleştirilmesi
Kullanım Alanı
Dinamik sistemler
Diferansiyel denklemler
Uygulamalı matematik
Fizik, mühendislik, biyoloji modellemeleri
Lisans + yüksek lisans düzeyi
1. Problemin Tanımı
Birçok matematik bölümü öğrencisi, karmaşık diferansiyel denklem sistemlerinin çözümünde:
Kapalı form çözümler bulmakta
Sayısal çözümleri doğrulamakta
Faz uzayı analizleri yapmakta
Stabilite noktalarını belirlemekte
Modelin parametreye duyarlılığını test etmekte zorlanır.
Wolfram Mathematica bu alanlarda tek araçla tüm süreci kapsayan bir çözümdür.
2. Örnek Model: Lotka–Volterra Sisteminin Analizi
ODE sistemi:
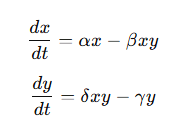
Bu modele ait:
sabit noktalar
stabilite
faz portreleri
simülasyonlar
parametrik duyarlılık tek notebook içinde yapılabilir.
3. Wolfram Mathematica Kullanımı
✔ Sabit Noktaların Hesabı
Solve[{α x - β x y == 0, δ x y - γ y == 0}, {x, y}]
✔ Faz Portresi
StreamPlot[{α x - β x y, δ x y - γ y}, {x, 0, 5}, {y, 0, 5}]
✔ Numerik Simülasyon
sol = NDSolve[
{x'[t] == α x[t] - β x[t] y[t],
y'[t] == δ x[t] y[t] - γ y[t],
x[0] == 1, y[0] == 1},
{x, y}, {t, 0, 20}
]
✔ Zaman Serisi Grafik
Plot[{x[t] /. sol, y[t] /. sol}, {t, 0, 20}]
✔ Parametre Duyarlılık Analizi (Manipulate ile)
Manipulate[
Plot[{x[t] /. sol, y[t] /. sol}, {t, 0, 30}],
{{α, 1}, 0.1, 3},
{{β, 0.1}, 0.01, 1},
{{γ, 1}, 0.1, 3},
{{δ, 0.1}, 0.01, 1}
]
4. Matematik Bölümleri İçin Fayda
Öğrenciler dinamik sistemleri tek ekranda simüle ederek öğrenir
Hızlı modelleme → araştırma projelerinde büyük zaman kazancı
Parametrik analiz → yüksek lisans & doktora çalışmalarında güçlü altyapı
Daha önce elle yapılamayacak karmaşıklıkta simülasyonlar
