Mathematica ile büyük matrislerde özdeğer çözümleri, diagonalizasyon ve spektral analiz

Kullanım Alanı

• Lineer cebir

• Matematiksel fizik

• Sayısal analiz

• Makine öğrenimi alt yapıları

• Algoritma teorisi

1. Problemin Tanımı

Özdeğer–özvektör hesapları matematiğin temelidir; ancak:

• Büyük matrislerde hesap zordur

• Sembolik + sayısal birlikte çalıştırmak güçtür

• Manual doğrulama neredeyse imkânsızdır

• Spektral analiz için interaktif görselleştirme gerekir

Mathematica bu süreçleri basitleştirir ve hızlandırır.

2. Örnek Matris

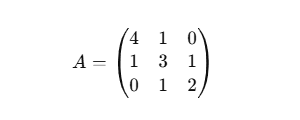
3. Wolfram Mathematica Kullanımı

✔ Özdeğer ve Özvektörler

Eigensystem[A]

✔ Diagonalizasyon Testi,

DiagonalizableMatrixQ[A]

✔ Spektral Ayrışım

SpectralDecomposition[A]

✔ Sembolik Hesap

Eigensystem[{{a,1},{1,b}}]

✔ Manipulate ile Matris Parametrelerinin Etkisini Görselleştirme

Manipulate[

MatrixPlot[{{a,1},{1,b}}],

{{a,0,10}}, {{b,0,10}}

]

4. Ek Uygulama — Grafik Teorisine Geçiş

Özdeğer hesapları grafik teorisinde önemli bir rol oynar.

Bir bölüm öğrencisi, Mathematica ile:

GraphPlot[RandomGraph[20]]

LaplacianEigenvalues[RandomGraph[20]]

gibi işlemlerle hem matris teorisini hem de grafik Laplasyanlarını inceleyebilir.

5. Matematik Bölümleri İçin Fayda

• Lineer cebir derslerinde interaktif öğrenme

• Büyük boyutlu matrislerde dakikalar yerine saniyeler içinde çözüm

• Matematiksel fizik ve makine öğrenimi için temel altyapı

• Sembolik + sayısal hesapları tek platformda gerçekleştirir.

Bu Use-Case’ler Üniversite Matematik Bölümleri İçin Ne Sağlar?

• Ders içerikleri modernleşir.

• Araştırma süreçleri hızlanır.

• Öğrencilerin matematiksel sezgisi artar.

• Bölüm, uluslararası standartlarda yazılım altyapısına kavuşur.

• Matematiğin soyut kavramları somut hâle gelir.